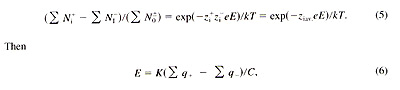|
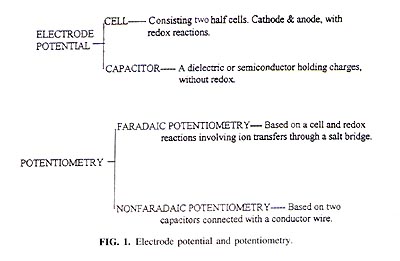
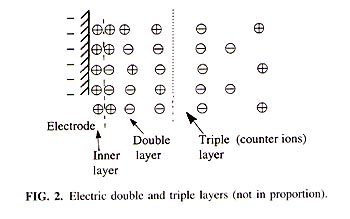
Explanation of Misleading Nernst Slope by Boltzmann Equation K. L. Cheng Department of Chemistry, University of Missouri-Kansas City, Kansas City, Missouri 641 10 Received March 12. 1998; accepted March 23, 1998 The common misuse in the literature of the terms Nernst slope, Nernst factor, and Nernst potential should be corrected. The membrane electrode potential is explained by the Boltzmann distribution equation. The slope of 59 mV per ionic unit is not unique to the Nernst equation. Both the Nernst equation and the Boltzmann distribution equation give the same 59-mV slope based on different mechanisms. The slope indicates only the change of -D G regardless of mechanisms. To avoid any misleading inference to the wrong equation mechanism, a person's name should not be used to denote a common lope. The factors affecting the slope, the electrode potential and itís measurements, the importance of potential mechanism, and the modified Boltzmann equation are presented. INTRODUCTION There have been widespread misconceptions about the application of the Nernst equation to explain the mechanism of pH glass electrodes and ion selective electrodes (ISE). The terms Nernst slope (5, 12, 13). Nernst factor (5, 9, 15). and Nernst potential (5) have been commonly misused in the literature. An electrode potential may he divided, at least, into two types of electrode potential. One is the cell potential consisting of two half-cells, cathode and anode, with redox reactions such as a Zn in a ZnCI2 solution; the other is the capacitance potential based on the adsorption of charges or ions on a dielectric or semiconductor such as a glass without redox reactions. Potential measurement may be divided into two types of potentiometry", namely, faradaic potentiometry and nonfaradaic potentiometry (1, 2). The former is based on a device consisting of two half cells with a salt bridge for the potential measurements and the latter is based on a device with a dielectric or semiconductor adsorbed with charged particles or ions against a reference electrode; a conducting wire instead of a salt bridge is commonly used. A salt bridge can also function as a conducting wire for electron transfers; however, a conducting-wire cannot substitute for the salt bridge for ion transfers (see fig. 1). The reasons for the misuse of the Nernst equation have been explained in the literature (1, 2). ELECTRODE POTENTIAL MECHANISM The electrode mechanism based on the Nernst equation. redox reaction. is representedE = E?/font> + 2.3 RT/nF log([Ox]/[Red]). (1) The electrode mechanism based on the double and triple layers of a capacitor is shown in Fig. 2.
BOLTZMANN DISTRIBUTION EQUATION The Boltzmann distribution equation can be written as follows: Ni / N0 = exp{(-Zi eE) / kT} (2)The electrode potential is measured with respect to the bulk solution. The following quantities are found: zi = 1 (for H+); e = 1.6 x 10-19, electron charge; k = 1.38 x 10-23, Boltzmann constant: T = 298 at 25 ?/font> C. The above equation will become E = 2.3 kT /?/font> (zi e log(Ni /N0)) = ?/font> 0.059 log(Ni /N0 ), (3) where Ni is ions or charge particles on the electrode surface in charge density and No is ion concentration in bulk solution, Here 2.3 RT / nF = 2.3 zie / kT = 59 mV/pC = -D G. (4) The adsorption of protons onto an insulator in an acidic solution with a Helmholtz double layer is described as the Helmholtz potential, which decreases about 60 mV per pH unit (3). In die electron transfer expressions, the expression exp(-(Etl - EF) / kT) based on the -D G change is called the Fermi function (3), All the slopes are 59 mV based on D G for different mechanisms. This causes some confusion. Now we can see why we should not denote a slope with a particular person's name for the same D G that is not unique to any mechanism. What is important is the mechanism, not the slope. It is clear that the slope does not explain the mechanism, We may suggest that the slope for the pH glass electrode and ISE be called the capacitance slope, as it is related to the capacitance potential (4). MODIFIED BOLTZMANN EQUATION In pH and ISE potential measurements, when both cations and anions are adsorbed at the same time onto an electrode surface, such as a pH glass electrode or an Ag2S electrode (9), we call the capacitor a zwitterionic capacitor. The original Boltzmann equation is for an electrode with a single type of ion. Now for an electrode with a mixture of positive and negative charges, the Boltzmann equation may be modified as follows:
where q is charge density, C is capacitance, and K is a constant. FACTORS AFFECTING THE SLOPE In dealing with the pH glass electrode and ISE, the following factors are found to affect the electrode potentials:
These factors affect the slope but do not change the mechanism. At pH 6-8, the pH glass electrode shows a nonlinear curve, not like what the Nernst equation predicts or what most people expect. The Nernst equation cannot he applied to most anions, such as OH- , which plays a dominant role in the glass electrode potential development in basic media (11). The resulting curve shown for Ag+ by the Ag2S electrode was actually for both the Ag+ and the anion ligands. it was misleading by the Nernst equation and its slope (9). The number 0.059 V for the Nernst slope has been quoted by most textbooks; however, a few textbooks quoted 0.0591, 0.05915 (12), 0.05916 (13), and 0.0591594 (16), possibly for better accuracy. The authors forgot the meaning of significant figures, As discussed previously, the slope is affected by many factors. To have more significant figures for the slope not only does not mean much, but also misleads to support the high accuracy of the reaction mechanism. This number with many decimals is just another calculation number (14). MECHANISM AND THERMODYNAMICS The mechanism is most important for understanding the electrode process and potential origin. The thermodynamics shows only the D G. the energy change, not the mechanism. In the textbooks of quantitative analysis and electroanalytical chemistry, the thermodynamics has been overemphasized, neglecting the mechanism. A correct mechanism should be based on careful experimental data. A slope does not affect the mechanism, but a mechanism sometimes affects the slope. It is improper to name a common slope after a particular person, suggesting incorrectly that the slope is unique for that mechanism and that when the calculated slope matches the experimental data, then the mechanism must be correct. This paper has proved that other equations also give the same 59-mV slope based on different mechanisms. CONCLUSIONS The Nernst equation has been misused in studies with membrane electrodes, including the pH glass electrode and ISE electrodes. There is no such thing as the Nernst slope, Nernst factor, or Nernst potential. First of all, the Nernst equation is not related to the capacitance potential. Second, a common slope, 59 mV, may be calculated from other equations from different mechanisms. It is also improper to name the slope the Nernst slope. the Boltzmann slope, or the Fermi slope, and the potential the Boltzmann potential, the Helmholtz potential, or the Nernst potential. The potential origin of membrane electrodes comes from the adsorption of charged ions or particles on the electrode surface, following the Boltzmann distribution, capacitance law. E = q /C. and Fruendlich isotherm. Contrary to what's shown in the Nernst equation, that the slope is infinitely linear, E = q/C is linear only in a limited range depending on the nature of ions, the electrode surface and thickness, etc. Here, the usefulness of a mechanism or theory depends on how good it can explain the electrode potential phenomena. If it cannot explain important facts, then it should either be revised or disposed of. It is a capital mistake to theorize before one has data. We have recently found that the IUPAC conventional redox mechanisms of calomel and Ag/AgC] reference electrodes have been erroneously postulated on the basis of the Nernst equation and Nernst slope (10). This is another example of the second Nernst hiatus (2). ACKNOWLEDGMENT We thank Jerry Y. C. Jean for his assistance and the K. L, Cheng Trust for financial support. REFERENCES
|